It is not a difficult task to divide one pizza into 2 or 4 or 8 equal parts. But, suppose that you have invited 11 guests on the party and you bought 11 pizzas, but you forgot a pizza for yourself? Will you be ready to give up your share or will you make an effort to divide 11 pizzas into 12 equal amounts? How will you do that? Since everybody has to take 11/12 of one pizza, you may decide to divide each pizza into 12 equal pieces and then to give to each person 11 pieces. In that case you have to make at least 11 × 6 = 66 cuts, since one pizza can be divided into 12 equal pieces by at least 6 cuts. The other thing is that the pieces that you will get will be a little more bigger then a half of a piece that is 1/8 of a pizza. You can imagine that size by looking at the below picture of a pizza divided into 8 equal parts. Estimated level: 4th Grade Math.
The ancient Egyptian mathematics gives us a better solution of this problem using the Egyptian fractions. Before explaining what are Egyptian factions, let us first explore the ancient Egyptian numeral system.
It is belived that the ancient Egyptians had the very first fully developed decimal numeral system (around 2700 BC). They used seven different symbols for the first seven powers of 10, and numbers were formed by repeating these symbols as many times as needed.

What is more fascinating about Egyptian numerals is the way the fractions were written. The ancient Egyptians did not have a single notation for a fraction with a nominator greater than 1. They only had (with a few exceptions) notations for unit fractions. The "R" hieroglyph was placed above a number to represent its reciprocal value. Then, by "adding" these unit fractions they obtain any other fraction. For example, the fraction 5/8 was written as 1/2 + 1/8 like this:
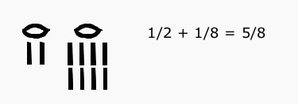
Our first example already has two representations as Egyptian fraction which indicates that it is better to have a procedure or a method for building the Egyptian fractions rather than guessing the representation. Fibonacci, in 1202, was the first who described a very simple method for Egyptian fractions called the Greedy algorithm, which works when all other methods will fail. In each step, the Greedy algorithm chooses the biggest unit fraction that is less or equal to the remanding fraction that needs to be expanded. The reminding fraction is formed by subtracting the chosen unit fraction from the fraction that needs to be expanded. This process is repeated until the reminding fraction becomes a unit fraction.
We will illustrate the Greedy algorithm on the fraction 11/12, in order to give the answer to our initial question "How to divide 11 pizzas between 12 people equally?".
1. The biggest unit fraction that is less or equal to 11/12 is 1/2, so we subtract these fractions to get the reminding fraction:
The ancient Egyptian mathematics gives us a better solution of this problem using the Egyptian fractions. Before explaining what are Egyptian factions, let us first explore the ancient Egyptian numeral system.
Egyptian numeral system
It is belived that the ancient Egyptians had the very first fully developed decimal numeral system (around 2700 BC). They used seven different symbols for the first seven powers of 10, and numbers were formed by repeating these symbols as many times as needed.
Image by Mark Millmore

Image by Mark Millmore
With help of the above examples, try to write with Egyptian numerals the following numbers: 25, 104, 2452, 40404, your age, year of your birth or the current year.
Egyptian fractions
What is more fascinating about Egyptian numerals is the way the fractions were written. The ancient Egyptians did not have a single notation for a fraction with a nominator greater than 1. They only had (with a few exceptions) notations for unit fractions. The "R" hieroglyph was placed above a number to represent its reciprocal value. Then, by "adding" these unit fractions they obtain any other fraction. For example, the fraction 5/8 was written as 1/2 + 1/8 like this:
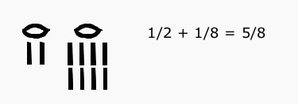
This notation of a fraction as a sum of different unit fractions is called an Egyptian fraction. This representation is not unique. The fraction 5/8 can be also represented as 1/2 + 1/10 + 1/40, but not as 1/4 + 1/4 + 1/8, since all fractions in the representation should be different. Can you find another representation of the fraction 5/8 as an Egyptian fraction?
The greedy algorithm for Egyptian fractions
Our first example already has two representations as Egyptian fraction which indicates that it is better to have a procedure or a method for building the Egyptian fractions rather than guessing the representation. Fibonacci, in 1202, was the first who described a very simple method for Egyptian fractions called the Greedy algorithm, which works when all other methods will fail. In each step, the Greedy algorithm chooses the biggest unit fraction that is less or equal to the remanding fraction that needs to be expanded. The reminding fraction is formed by subtracting the chosen unit fraction from the fraction that needs to be expanded. This process is repeated until the reminding fraction becomes a unit fraction.
We will illustrate the Greedy algorithm on the fraction 11/12, in order to give the answer to our initial question "How to divide 11 pizzas between 12 people equally?".
1. The biggest unit fraction that is less or equal to 11/12 is 1/2, so we subtract these fractions to get the reminding fraction:
11/12 - 1/2 = 11/12 - 6/12 = 5/12.
2. Now, the biggest unit fraction that is less or equal to the reminding fraction 5/12 is 1/3, since 1/3 = 4/12 < 5/12, and 1/2 = 6/12 > 5/12. We subtract 1/3 from 5/12:
5/12 - 1/3 = 5/12 - 4/12 = 1/12.
3. The reminding fraction is a unit fraction 1/12, so the algorithm is over and we have a representation of 11/12 as an Egyptian fraction:
11/12 = 1/2 + 1/3 + 1/12.
This means that each person will get 1/2, 1/3 and 1/12 of a pizza, and this is more practical to obtain, since we have to half 6 pizzas (with 6 cuts), then we have to cut 4 pizzas into thirds (with 12 cuts) and one pizza into 12 equal pieces (with 6 cuts). So, we have to make 24 cuts which is significantly less then 66 cuts, if we decided to cut each pizza into 12 equal pieces.
Now it is your turn, use the Greedy algorithm to represent the fractions 2/7, 17/19 and 123/155 as Egyptian fractions or find out how to divide 4 apples between 5 people equally.


It would be more optimal if we cut the pizzas in the following order: 1/2 * 6 + 1/4 * 3 + 1/6 * 2
ReplyDeleteThis way, 12 persons will get: 1/2+1/4+1/6 and we will have 6*1 + 3*2 + 2*3 cuts or 18 cuts altogether.
Also, cutting a pizza in 3 parts is similar to cutting 1/12 of one pizza.
N.V.
Viktor, first thank you for your interest in this new blog and thank you for your comment.
DeleteYou are right. Obviously, in this case, the Greedy algorithm did not give the optimal minimal number of cuts, but it is still less then 66 cuts. It will be interesting to discuss further, if your answer is the most optimal, it looks that it is, but we need a proof.
About your last statement, "cutting a pizza in 3 parts is similar to cutting 1/12 of one pizza", I suppose you are discussing the difficulty of estimating 1/3 and 1/12, because cutting a pizza into thirds needs 3 cuts, and cutting 1/12 of one pizza needs 2 cuts, if I am not wrong.
Thanks again for your comment.